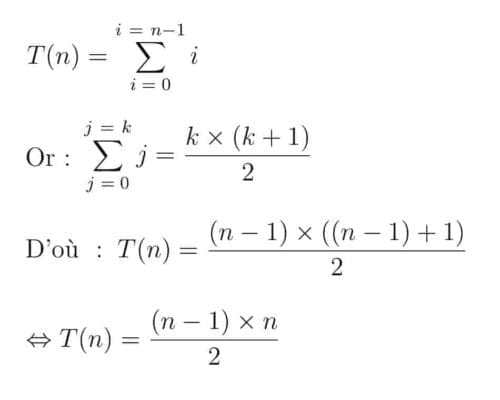[pulsar]

a) 1260 « tchin-tchin ».

b) 630 « tchin-tchin ».

c) 153 « tchin-tchin ».

d) Oui, on peut trouver une formule générale pour n convives dans le cas où ils ne trinquent qu’une seule fois. (On peut aussi trouver une formule dans le cas où ils trinquent p fois…)

😇

[Membre Inconnu]

Salut Norbert

Annie et ses amis ne respectent apparemment pas les règles de distanciation sociale 😉

C’est bien plus facile de calculer la réponse de la question b), il suffit ensuite de doubler pour la réponse à la question a). Pour la question b), j’ai fait des additions mais j’imagine qu’il doit y avoir une manière plus simple de calculer (la fameuse formule!), et surtout qui n’implique pas le risque de se planter sur les touches de la calculette (j’ai dû refaire le calcul parce que je trouvais pas le même résultat que Pulsar).

Je ne vois pas l’intérêt de chercher la réponse à la question c), c’est le même principe que la question b).

Belle journée!

[Membre Inconnu]

@pulsar

Oui, on peut trouver une formule générale pour n convives dans le cas où ils ne trinquent qu’une seule fois. (On peut aussi trouver une formule dans le cas où ils trinquent p fois…)

Heureux de te revoir, pourrais tu détailler, stp?

[Membre Inconnu]

@lau2pluie

Annie et ses amis ne respectent apparemment pas les règles de distanciation sociale!

Ni la distance du maître !

[Membre Inconnu]

@grandadais

Je pense que pulsar a utilisé le coefficient binomial, je te laisse voir ce que c’est.

faisons pour les gens de “mon bar” (d’autant plus qu’ils sont direectement concernés par les chin-chin)

Anne trinque avec 35 personnes, donc ça fait 35 chin-chin ! (jusque là mon bar suit)

Si chaque convive veut trinquer de son initiative avec les autres (sans s’occuper de savoir si les autres ont déjà trinqué avec lui ou pas), chaque convive est dans la même situation qu’Anne

donc ça fat 36 fois 35 chin-chin !

Donc nombre de chin-chin si les gens trinquent 2 fois: 36 x 35

et si ils ne trinquent qu’une fois, la moitié: donc [36 x 35 ]/ 2 =

formule générale

pour 2 chin chin par couple, si n convives: n x (n-1)

pour un chin chin par couple: si n convives: [n x (n-1)]/2

PS mon bar:

https://www.google.com/maps/@43.1098033,5.9402358,3a,75y,24.25h,84.47t/data=!3m7!1e1!3m5!1sSvE7TYVEy0iJ_kaQeAsOhw!2e0!6s%2F%2Fgeo0.ggpht.com%2Fcbk%3Fpanoid%3DSvE7TYVEy0iJ_kaQeAsOhw%26output%3Dthumbnail%26cb_client%3Dmaps_sv.tactile.gps%26thumb%3D2%26w%3D203%26h%3D100%26yaw%3D114.684555%26pitch%3D0%26thumbfov%3D100!7i13312!8i6656

[Membre Inconnu]

C’est effectivement plus simple que ma méthode par addition.

[pulsar]

Anne trinque avec 35 personnes, donc ça fait 35 chin-chin ! (jusque là mon bar suit)

Si chaque convive veut trinquer de son initiative avec les autres (sans s’occuper de savoir si les autres ont déjà trinqué avec lui ou pas), chaque convive est dans la même situation qu’Anne

donc ça fait 36 fois 35 chin-chin !

Donc nombre de chin-chin si les gens trinquent 2 fois: 36 x 35

et si ils ne trinquent qu’une fois, la moitié: donc [36 x 35 ]/ 2 = formule générale

pour 2 chin chin par couple, si n convives: n x (n-1)

pour un chin chin par couple: si n convives: [n x (n-1)]/2

Pas du tout ! Le résultat est bon, certes, mais l’explication est complètement fausse.

Voilà la bonne explication :

• On choisit un convive (n’importe lequel). Il va donc pouvoir trinquer avec les 35 autres une fois. À ce stade on a donc 35 « tchin-tchin » de comptabilisés.
• On choisit un autre convive (toujours n’importe lequel) parmi ceux qui n’ont pas encore été choisis (très important pour éviter les doublons de comptage !). Ce deuxième convive va donc pouvoir trinquer avec les 34 autres avec qui il n’a pas encore trinqué. À ce stade on a donc 35 + 34 = 69 « tchin-tchin » de comptabilisés.
• À la troisième itération, toujours avec les mêmes conditions (on prend un convive qui n’a pas encore été choisi et on compte le nombre de personnes avec lesquelles il n’a pas encore trinqué, ici 33 convives restants. À ce stade on a donc 35 + 34 + 33 = 102 « tchin-tchin » de comptabilisés.
• …
• Et ainsi de suite jusqu’au dernier convive pour qui le nombre de personnes avec qui il n’a pas encore trinqué est égal à 0 (vu qu’il ne reste plus que lui…).

Le total des « tchin-tchin » est donc : 35 + 34 + 33 +32 + 31 + … + 5 + 4 + 3 +2 + 1 + 0 = 630 « tchin-tchin ».

On en déduit que le nombre de « tchin-tchin » (noté T(n) ci-après) en fonction du nombre de convives est donné par la formule suivante (cf image ci-jointe) :

[pulsar]

Et je précise que si dans la formule de T(n), on s’arrête à n-1 et non à n, c’est parce qu’on considère qu’une personne ne peut pas trinquer avec elle-même ! (Sauf à avoir deux verres simultanément, mais c’est un autre problème…)

[Membre Inconnu]

@grandadais

qui cherche trouve, souviens-toi des équations différentielles

@pulsar

mais l’explication est complètement fausse.

Et moi qui me réjouissais de te voir revenir, c’était pour le 2e coup de couteau!

Ce n’est pas l’avis de la personne avant toi (un peu de politesse, de savoir vivre, que diantre! Toi aussi, tu cherches, tu trouves.)

@pulsar

d’une part tu as fais une démonstration partielle, “et ainsi de suite” pour le 1er convive, 2e convive, mais on a vu dans le thread “somme des n premiers nombres impairs” que ce n’est pas parce que un résultat est vrai pour un entier, et que s’il est vrai pour un entier il est vrai pour le suivant, qu’il est automatiquement vrai pour tous les entiers concerné. Pour obtenir ce résultat, il faut faire appel aux axiomes de Peano qui définissent N, ce que tu n’as pas fait

Axiomes de Peano

0 est un entier naturel (donc l’ensemble des entiers naturels n’est pas vide).

Tout entier naturel n a un successeur, noté s(n) ou Sn.

<i style=”font-family: inherit; font-size: inherit;”>Aucun entier naturel n’a 0 pour successeur (l’ensemble des naturels a un premier élément).

Deux entiers naturels ayant même successeur sont égaux.

Si un ensemble d’entiers naturels contient 0 et contient le successeur de chacun de ses éléments alors cet ensemble est égal à ℕ

@pulsar

D’ou sors tu que la somme des k+1 premiers entiers ( de 0 à k) vaut [k x (k+1)]/2

c’est le théorème de Mandrake-le-magicien ?

[Membre Inconnu]

Hey, salut tous !
Moi je ne connais pas Mandrake-le-magicien, mais j’aime beaucoup cette démo de la somme des premiers entiers (et pour une fois, oublions le zéro, il ne sert pas à grand chose dans cette somme ) : Notons la S (quel choix original :/)
S = 1 + 2 + …. + k + … + (n-1) + n
S = n + (n-1) + … + (n-k+1) + … + 2 + 1
Puis en sommant terme à terme on obtient :
2S = (n+1) + (n+1 + … + (n+1) + …. + (n+1) + (n+1) (avec n termes dans cette somme)
Donc 2S = n (n+1). D’où : S = ….
[Bon avec les Sigma, les changements d’indice et tout et tout, c’est encore plus fun !]
On peut aussi jouer à faire des pyramides de rouleaux de PQ (par exemple) (ici représentés par des 0 (ha ben si, il sert à quelque chose finalement ! )) pour s’en convaincre (ici avec n=5).
0 00000
00 0000

000 et on accole la même pyramide à l’envers 000

0000 (bon ok, elle tient moins facilement) 00

00000 0

Puis on se rend compte que c’est lié à la formule d’un triangle rectangle de base n+1 et de hauteur n. (Et là, on sait qu’on se rappellera cette sublime formule à tout jamais, yes !)
Puis si on n’a plus de PQ (grrrr, merci Covid !) on peut aussi colorier des petites cases d’un cahier 24*32, 96 pages, petits carreaux.